

|
 |
||
|
This article belongs to the series documenting the reasoning behind and development of new features in the Formal Methods Toolkit.
The previous article presented the Deduce feature, which allows to recover or extract knowledge from known quantified statements and transform it into knowledge about individual elements. For example, if it is known that all elements of the array are zero, then it is possible to “deduce” that a given element, say at index 5, is indeed zero and continue the reasoning with that newly available fact.
Explicit deductions like this show that knowledge in FMT exists at different levels - the core solver operates at the level of individual variables, whereas quantified statements provide knowledge at some higher structural level, which is not directly available to the solver. Deduction allows the knowledge to flow down from that higher level to the level of individual variables, but for completeness an additional mechanism is needed that will allow to feed knowledge upwards, from individual values to that of quantified statements. For example, if it is already known that array elements at indices from 1 to 5 are zero and it is also known that a particular element at index 6 is also zero, then it should be possible to feed that knowledge up to extend the existing quantified statement so that its scope is wider - that is, that elements from 1 to 6 are zero. Existential statements have their analogue as well, for example if it is known that there exists a zero value at indices from 1 to 5 and it is also known that 5 is not that index (that is, it has been established that this element is not zero), then feeding this knowledge up gives a new quantified statement that there exists a zero value at indices from 1 to 4.
The missing feature is naturally called “induction” and the new operation Induce fits the rest of the family. Here are some examples with ForAll:
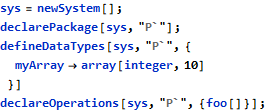

The proof statements show the accumulation of knowns in each step:

Steps 1. and 2. are straightforward - these are assumptions and are registered without verification. The induction at step 3. has the same grammar structure as deductions described in the previous article - that is, they refer to the already known quantified statement and indicate the point at which some new knowledge is being created. Previously, with deductions, the indicated point (like i->5) was an “instantiation” that extracted the knowledge from quantified statement to the level of individual value, but here it is an “extension” that injects the new knowledge to the higher level and allows to extend the existing quantified statement. This way a new statement is created (that’s the second entry for step 3. in the table above) and even though the region was not automatically transformed to nicely-looking 1<=i<=6, its meaning is as intended. From the mathematical perspective, a statement about N elements was extended to cover N+1 elements and this is the essence of induction.
All steps can be proved as usual:


As before, the only condition that was not proved (and which can be ignored in this article) is the initialization of local variable.
What is important here is that such operations can be cumulated in sequence or integrated with loop invariants, which will allow them to be used to reason about array operations.
Another example deals with Exists, where induction works in reverse direction - instead of widening the scope of the quantified statement, the knowledge about individual elements allows to narrowing the scope instead:

The above example demonstrates a single search step - at the beginning it is known that the interesting element is somewhere in the whole array, but a check allows to exclude an individual index from the scope, which in turn allows to narrow down the search in further steps. In order to make the exclusion more visible, the Not[...] construct is required in this kind of inductions.
The proof statements follow:


As with the previous example, step 1. is just an encoded assumption. Step 2. verifies the condition expression; step 3. is already within the conditional branch, where it is known (locally to that branch) that a[[1]]!=0. This allows to narrow down the Exists quantified statement, which is added to the list of knowns - again the new range was not nicely compressed to 2<=i<=10, but it has no impact on the ability of the system to reason about this narrower range. It is not harmful to have both old (wider) and new (narrower) statement in the same list and the user can refer to the one that is relevant in further proofs. What is important, though, is that at the end of the operation, when the conditional branch is left behind, the new quantified statement that originated within the conditional branch is no longer listed just aside the old one, but wrapped in a condition to properly track its origin. This works with nested conditional statements as well.
The next article will demonstrate how the quantified statements can be “initialized” and verified.